Consider the following personal finance problem. You are to be paid for a consulting job, for a total of C = $30, 000, over the next six months. You plan to use this payment to cover some past credit card debt, which amounts to D = $7000. The credit card's APR (annual interest rate) is r₁ = 15.95%. You have the following items to consider:

• At the beginning of each month, you can transfer any portion of the credit card debt to another card with a lower APR of r₂ = 2.9%. This transaction costs r₃ = 0.2% of the total amount transferred. You cannot borrow any more from either of the credit cards; only transfer of debt from card 1 to 2 is allowed.
• The employer allows you to choose the schedule of payments: you can distribute the payments over a maximum of six months. For liquidity reasons, the employer limits any month's pay to 4 /3 x (C/6).
• You are paid a base salary of B = $70,000 per annum. You cannot use the base salary to pay off the credit card debt; however, it affects how much tax you pay (see next).
• The first three months are the last three months of the current fiscal year and the last three months are the first three months of the next fiscal year. So if you choose to be paid a lot in the current fiscal year (first three months of consulting), the tax costs are high; they are lower if you choose to distribute the payments over several periods. The precise tax due depends on your gross annual total income G, which is your base salary, plus any extra income. The marginal tax rate schedule is given in Table 14.1.
• The risk-free rate (interest rate from savings) is zero.
• Time line of events: all events occur at the beginning of each month, i.e. at the beginning of each month, you are paid the chosen amount, and immediately you decide how much of each credit card to pay off, and transfer any debt from card 1 to card 2. Any outstanding debt accumulates interest at the end of the current month.
• Your objective is to maximize the total wealth at the end of the two fiscal years while paying off all credit card debt.

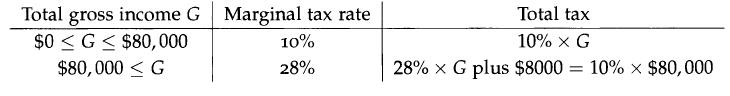
1. Formulate the decision-making problem as an optimization problem. 

Make sure to define the variables and constraints precisely.
To describe the tax, use the following constraint:

T_i = 0.1 min(G_i/, α) + 0.28 max(G_i — α, 0),

where T_i; is the total tax paid, G_i is the total gross income in years i = 1,2, and α = 80,000 is the tax threshold parameter.

2. Is the problem a linear program? Explain.

3. Under what conditions on oc and G; can the tax constraint (14.23) be replaced by the following set of constraints? Is it the case for our problem? Can you replace (14.23) by (14.26) in your problem?

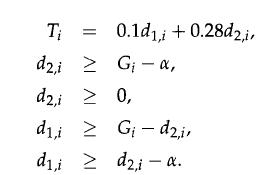
4. Is the new problem formulation, with (14.26), convex? Justify your answer.

5. Solve the problem using your favorite solver. Write down the optimal schedules for receiving payments and paying off/transferring credit card debt, and the optimal total wealth at the end of two years. What is your total wealth W?

6. Compute an optimal W for α ∈ [70k, 90k] and plot α vs. W in this range. Can you explain the plot?

Transcribed Image Text:

Total gross income G Marginal tax rate $0 G≤ $80,000 $80,000 G 10% 28% Total tax 10% X G 28% x G plus $8000 = 10% × $80,000