Consider the following problem, known as Boolean Least Squares:

Here, the variable is x ∈ Rⁿ, where A ∈ R^m,n and b ∈ R^m are given. This is a basic problem arising, for instance, in digital communications. A brute force solution is to check all 2n possible values of x, which is usually impractical.

1. Show that the problem is equivalent to

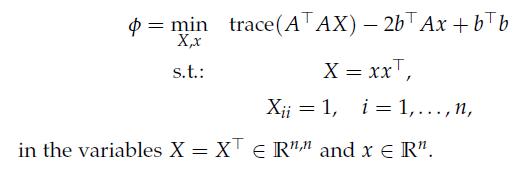
2. The constraint X = xx>, i.e., the set of rank-1 matrices is not convex, therefore the problem is still hard. However, an efficient approximation can be obtained by relaxing this constraint to , as discussed in Section 11.3.3, obtaining

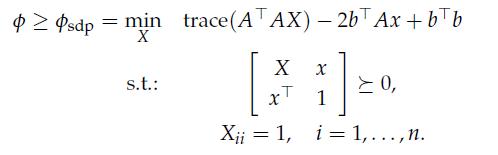
The relaxation produces a lower-bound to the original problem. Once that is done, an approximate solution to the original problem can be obtained by rounding the solution: x_sdp = sgn(x*), where x* is the optimal solution of the semidefinite relaxation.

3. Another approximation method is to relax the non-convex constraints x_i ∈ {–1, 1} to convex interval constraints –1 ≤ x_i ≤ 1 for all i, which can be written ΙΙxΙΙ≤ 1. Therefore a different lower bound is given by:

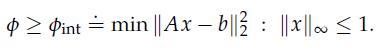
Once that problem is solved, we can round the solution by x_int = sgn (x*) and compare the original objective value

4. Which one of Φ_sdp and Φ_int produces the closest approximation to Φ? Justify carefully your answer.

5. Use now 100 independent realizations with normally distributed data, A ∈ R^10,10 (independent entries with mean zero) and b ∈ R¹⁰ (independent entries with mean 1). Plot and compare the histograms of of part 2, of part 3, and the objective corresponding to a naïve method where x_ls = sgn(A^TA)^–1 A^Tb) is the rounded ordinary Least Squares solution. Briefly discuss accuracy and computation time (in seconds) of the three methods.

6. Assume that, for some problem instance, the optimal solution (x, X) found via the SDP approximation is such that x belongs to the original non-convex constraint set {x : x_i ∈ {–1, 1}, i = 1, . . . , n}. What can you say about the SDP approximation in that case?

Transcribed Image Text:

¢ =min ||Ax − b||2 : x;€{−1,1}, i=1,...,n.