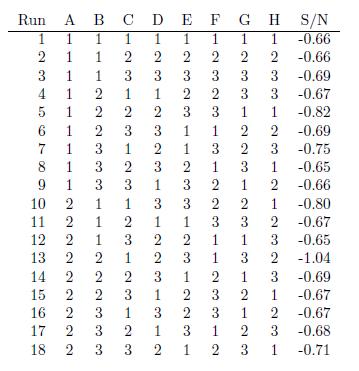
11. Kamohara et al. (2001) used an 18 run orthogonal fractional factorial to investigate the eect of
Question:
11. Kamohara et al. (2001) used an 18 run orthogonal fractional factorial to investigate the eect of 8 factors (372) upon the Vt variance of MOSFETs
(metaloxidesemiconductor eld-eect transistor). The list of factors and number of levels is shown below. The list of experiments and the response,

S/N, is shown in the table below. The purpose of the experiments was to nd factor level settings to maximize S/N.
(a) Read the data into SAS and create coded factor levels for the two-
level factor A and linear and quadratic contrasts variables for the three-
level factors in the SAS data step (i.e., if B=1 then do; Bl=-.707107;
Bq=.4082483; end; if B=2 then do; Bl=0; Bq=-.816497; end; etc.)
using the contrast coecients as shown in Section 2.8.1.
(b) Fit a regression model to the data using the coded factor levels for the two-level factor and the linear and quadratic contrast variables for each three-level factor in the design.
(c) Fit the model including only the ve independent variables with the highest absolute t-statistics that you found in (b).
(d) Fit the model that includes the coded factor levels for A, the linear contrast on C, the quadratic contrast on D, the interaction or product of the quadratic contrasts for B and D, the interaction or product of the linear contrast of F and the quadratic contrast on H, and experiment with a few other models of your choice.
(e) Do you think a plausible model can be found for the data after these 18 experiments? Why or why not?
Step by Step Answer:







