Erhardt (2007) ran a 28−4 fractional factorial experiment to determine the factors that aect ight time of paper helicopters. The standard design is shown in Figure 6.19 below with all dimensions in centimeters. The factors

and levels (in centimeters) he studied are shown in the table below. The low level on paper weight was phone book white pages paper, and the high level was standard copy paper. The fold direction was against (opposite to)
or with the direction of rotation.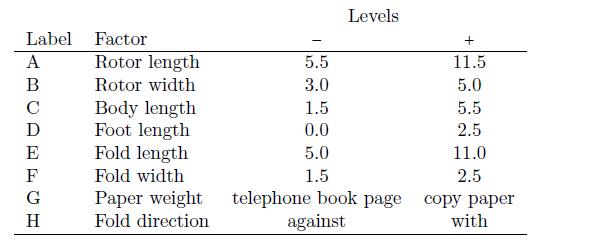

(a) What would you recommend for the generators of a 28−4 design?

(b) Create the design you recommend in

(a) and randomize the order of the runs. What is the experimental unit?

(c) List the aliases (up to three-factor interactions) for the 15 eects that can be estimated.

(d) Actually run the experiments by making the helicopters and timing them with a stopwatch.

(e) Calculate the eects (or regression coecients) and make a half-normal plot of the eects.

(f) Using the principle of eect heredity, try to determine what any strings of aliased two-factor interactions, that appear signicant on your plot, represent.
(g) Which factors would you include in a follow-up design to determine the combination of factor levels that produces the optimum ight time?

Transcribed Image Text:

Figure 6.19 Standard Helicopter Design B=4.0cm Rotor width A=8.5cm Rotor length Rotor Rotor C=3.5cm Body length Body E=8.0cm Fold length Fold Fold G = heavy/light paper H = with/against fold direction D= 1.25cm Foot F-2.0 cm Fold width Foot length