In the design of a thin lm redistribution layer (cited by J. Lorenzen, IBM Kingston and discussed by Lawson and Madrigal (1994)), the cir-

cuit impedance (Z) is a function of three design factors: the A, insulator thickness; B, linewidth; and C, line height as shown in Figure 12.21. From engineering rst principles, it can be shown that the impedance is given by Equation (12.10), where is the dielectric constant of the insulator and is assumed to be constant at 3.10.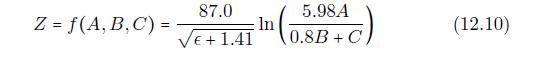

The nominal or mean values of A, B, and C can be specied by the design engineer, but in actual circuits these characteristics will vary from their nominal values due to manufacturing imperfections and wear during use.
The table above shows the feasible range and tolerance limits for these variables.

(a) Construct a control-factor array using a 23 factorial design.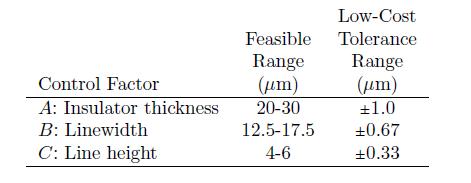

(b) Construct a noise-factor array (in deviations from the nominal settings in the control-factor array) using the table of Wang, Fang, and Lin.

(c) Evaluate Equation (12.10) for each combination of values in the product array, and calculate the mean and log variance impedance across the noise-factor array for each of the eight points in the control-factor array.

(d) Fit a model to the mean and log variance and identify the control fac-
tor settings that will make the impedance equal to 85 with minimum variability.

(e) Approximate the variance of Z, using the formula 2Z ‰ @f @AŽ2 2A +
‰ @f @B Ž2 2B + ‰ @f @C Ž2 2C (where 2A =tolerance range/6, etc.), and use nu-
merical optimization such as the optim function as described in Chapter 10 to minimize 2Z as a function of A, B, and C subject to the constraint that Z = 85 . Do the results dier substantially from the answer you got in (d)?

Transcribed Image Text:

87.0 5.98 A Z = f(A,B,C) = In (12.10) E+1.41 0.8B+C