In discussing how a planar wave propagates, we could turn our earlier argument around and say that for each point \(\mathrm{Q}\) in Figure 34.2 there is a point \(\mathrm{S}\) somewhere on the wavefront that radiates toward \(\mathrm{P}\) along a path exactly one wavelength longer than that from \(Q\), and therefore there should be a nonzero intensity at \(\mathrm{P}\). What is wrong with this argument?

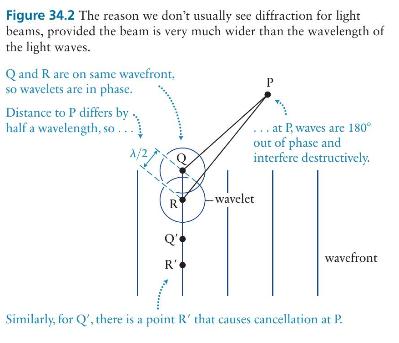
Figure 34.2 The reason we don't usually see diffraction for light beams, provided the beam is very much wider than the wavelength of the light waves. Q and R are on same wavefront, so wavelets are in phase. P Distance to P differs by half a wavelength, so... 1/2 -wavelet R Q' R' ...at P waves are 180 out of phase and interfere destructively. wavefront Similarly, for Q', there is a point R' that causes cancellation at P.