Consider a clamped uniaxial bar subjected to a tip load as shown in figure 8.9. Use three
Question:
Consider a clamped uniaxial bar subjected to a tip load as shown in figure 8.9. Use three elements of equal length to determine the tip displacement as a function of time. Use the central difference method for time integration and the consistent mass matrix. The properties of the bar are: \(E=100 \mathrm{GPa}, L=1 \mathrm{~m}, A=10^{-5} \mathrm{~m}^{2}, ho=4000 \mathrm{~kg} / \mathrm{m}^{3}\). The tip force is given by: \(F(t)=2 F_{\text {max }} t / t_{\max }\) for \(0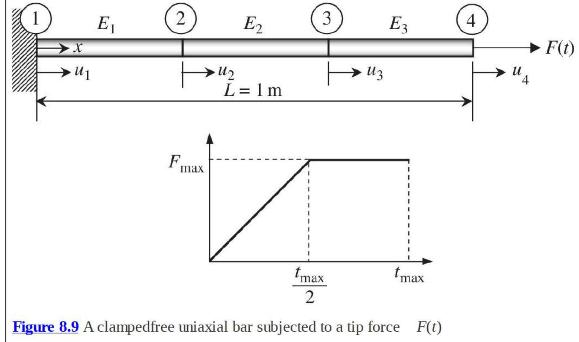
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Introduction To Finite Element Analysis And Design
ISBN: 9781119078722
2nd Edition
Authors: Nam H. Kim, Bhavani V. Sankar, Ashok V. Kumar
Question Posted:





