Instead of defining a reduced inertia (mu) to characterize the convertible kinetic energy of a system, we
Question:
Instead of defining a reduced inertia \(\mu\) to characterize the convertible kinetic energy of a system, we could define a reduced velocity \(v_{\text {red }}\) as follows: For a system of two particles, one of inertia \(m_{1}\) and velocity \(v_{1}\) and the other of inertia \(m_{2}\) and velocity \(v_{2}\), the kinetic energy is Derive an expression for the reduced velocity in terms of the given variables. (Just as the center-of-mass velocity is a weighted mean of the individual velocities, the reduced velocity is a weighted difference between the individual velocities.)
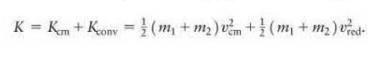
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:





