The transformation between position and time measurements in an inertial reference frame I and position and time measurements in a constantly accelerating (noninertial) reference frame \(\mathrm{N}\) is given by

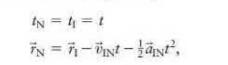
where \(\vec{v}_{\mathrm{IN}}\) is the velocity of the noninertial reference frame at \(t=0\) measured from the inertial reference frame and \(\vec{a}_{\mathrm{IN}}\) is the acceleration of the noninertial reference frame measured from the inertial reference frame. Derive by differentiation the transformation laws, giving \(v_{\mathrm{N}}\) and \(a_{\mathrm{N}}\) in terms of \(v_{1}\) and \(a_{1}\).

Transcribed Image Text:

IN-4-1 N-IN-IN,