You shoot a \(0.0050-\mathrm{kg}\) bullet into a \(2.0-\mathrm{kg}\) wooden block at rest on a horizontal surface (Figure P5.44). After hitting dead center on a hard knot that runs through the block horizontally, the bullet pushes out the knot. It takes the bullet \(1.0 \mathrm{~ms}\) to travel through the block, and as it does so, it experiences an \(x\) component of acceleration of \(-4.9 \times 10^{5} \mathrm{~m} / \mathrm{s}^{2}\). After the bullet pushes the knot out, the knot and bullet together have an \(x\) component of velocity of \(+10 \mathrm{~m} / \mathrm{s}\). The

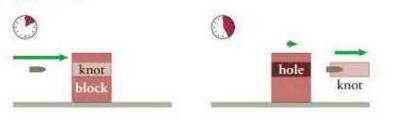
knot carries \(10 \%\) of the original inertia of the block.

(a) What is the initial velocity of the bullet?

(b) Using conservation of momentum, compute the final velocity of the block after the collision.

(c) Calculate the initial and final kinetic energies of the block-knot-bullet system. Does the kinetic energy of the system change during the collision?

(d) Can you calculate the coefficient of restitution for this collision? Which type of collision is it?

Transcribed Image Text:

knot block hole knot