In this problem, you will solve for the total energy eigenfunctions and eigenvalues for an electron in a finite depth box. We first go through the calculation for the box parameters used in Figure 16.1. You will then carry out the calculation for a different set of parameters. We describe the potential in this way:

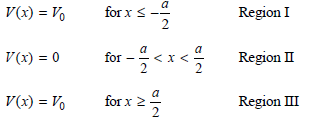
The eigenfunctions must have the following form in these three regions:

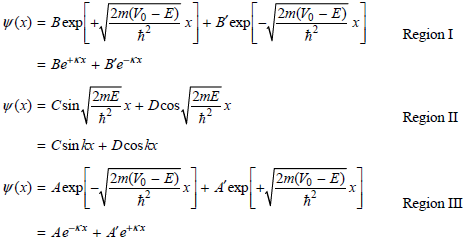
So that the wave functions remain finite at large positive and negative values of x, A€² = B€² = 0. An additional condition must also be satisfied. To arrive at physically meaningful solutions for the eigenfunctions, the wave functions in the separate regions must have the same amplitude and derivatives at the values of x = a/2 and x = ˆ’a/2 bounding the regions. This restricts the possible values for the coefficients A, B, C, and D. Show that applying these conditions gives the following equations:

These two pairs of equations differ on the right side only by the sign of one term. We can obtain a set of equations that contain fewer coefficients by adding and subtracting each pair of equations to give

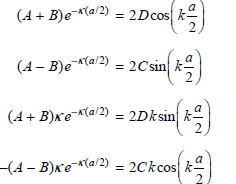
At this point we notice that by dividing the equations in each pair, the coefficients can be eliminated to give

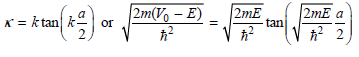
And

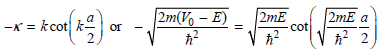
Multiplying these equations on both sides by a/2 gives dimensionless parameters, and the final equations are

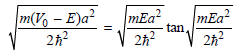
And

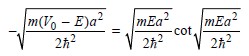
The allowed energy values E must satisfy these equations. They can be obtained by graphing the two sides of each equation against E. The intersections of the two curves are the allowed energy eigenvalues. For the parameters in the caption of Figure 16.1, V₀ = 1.20 × 10^-18J and a = 1.00 × 10^ˆ’9 m, the following two graphs are obtained:

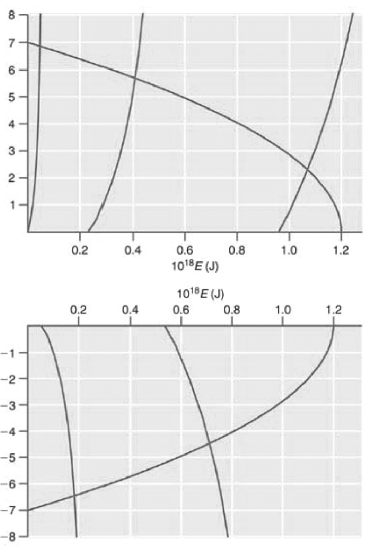
The five allowed energy levels are at 4.61 × 10^ˆ’20, 4.09 × 10^ˆ’19, and 1.07 × 10^ˆ’18 J (top figure), and 1.84 × 10^ˆ’19 And 7.13 × 10^ˆ’19 J (bottom figure).

a. Given these values, calculate λ for each energy level. Is the relation λ = 2a/n (for n an integer) that arose from the calculations on the infinitely deep box still valid? Compare the values with the corresponding energy level in the infinitely deep box. Explain why the differences arise.

b. Repeat this calculation for V₀ = 5.00 × 10 J and a = 0.900 × 10^ˆ’9 m. Do you think that there will be fewer or more bound states than for the problem just worked out? How many allowed energy levels are there for this well depth, and what is the energy corresponding to each level?

Region I for x s V(x) = V. 2 Region II V(x) = 0 for for x 2 Region III V(x) = Vo 2m(Vo E) 2m(Vo E) (x) %3D p| +, x+ B'exp Region I e* + 2mE w (x) = Csin, -x + Dcos, Region II = Csin kx + Dcoskx y(x) = Aexp 2m(Vo - E) x+ A exp +, 2m(Vo E) Region II = Ae ** + A'e*+*x -A'X