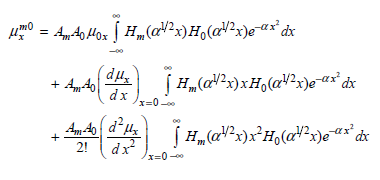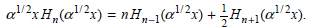Overtone transitions in vibrational absorption spectra for which Δn = +2, + 3, €¦ are forbidden for the harmonic potential V = (1 2)kx²because μ^mn_x= 0 for ˆ£m ˆ’ nˆ£ ‰  1 as shown in Section 19.4. However, overtone transitions are allowed for the more realistic anharmonic potential. In this problem, you will explore how the selection rule is modified by including anharmonic terms in the potential. We do so in an indirect manner by including additional terms in the expansion of the dipole moment μ_x(x) = μ_0x+ x (dμ_x/d x)_re, +€¦ but assuming that the harmonic oscillator total energy eigenfunctions are still valid. This approximation is valid if the anharmonic correction to the harmonic potential is small. You will show that including the next term in the expansion of the dipole moment, which is proportional to x², makes the transitions Δn = ±2 allowed. 

a. Show that Equation (19.8) becomes

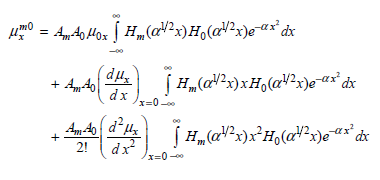
b. Evaluate the effect of adding the additional term to μ _x ^mn. You will need the recursion relationship

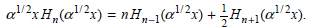
c. Show that both the transitions n = 0 †’ n = 1 and n = 0 †’ n = 2 are allowed in this case.

Transcribed Image Text:

0 = 44, Hoz H„(a?;)Ho(aV?x)e«x*dx (du + A4o [ H„(aV?x)xHo(@V²x)e-ax dx dx x=0-00 dx? x=0 -00 2! |a"?xH„(a?x) = nH„-1(@!/2x) + ¿Hp+1(a!/?x). 1/2.