The energy of rotation about a single bond is a periodic function of the torsion angle, ˆ…, and is, therefore, appropriately described in terms of a truncated Fourier series, the simplest acceptable form of which is given by

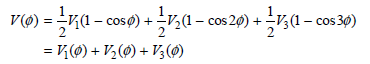
Here, V₁ is the one-fold component (periodic in 360º), V₂ is the two-fold component (periodic in 180º), and V₃ is the three-fold component (periodic in 120º).

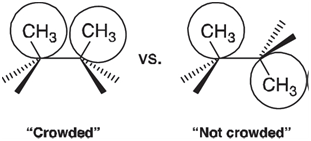
A Fourier series is an example of an orthogonal polynomial, meaning that the individual terms which it comprises are independent of each other. It should be possible, therefore, to dissect a complex rotational energy profile into a series of N-fold components and to interpret each of these components independent of all others. The one-fold component is quite easy to rationalize. For example, the one-fold term for rotation about the central bond in n-butane no doubt reflects the crowding of methyl groups,

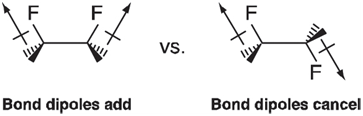
Whereas the one-fold term in 1, 2-difluoroethane probably reflects differences in electrostatic interactions as represented by bond dipoles:

The three-fold component represents the difference in energy between eclipsed and staggered arrangements about a single bond. However, the two-fold component is perhaps the most interesting of the three and is what concerns us here. It relates to the difference in energy between planar and perpendicular arrangements.

Optimize the geometry of dimethyl peroxide (CH₃OOCH₃) subject to the COOC dihedral being held at 0°, 20°, 40°, . . . , 180° (10 optimizations in total). Use the B3LYP/6-31G* density functional model. Construct a plot of energy versus dihedral angle and fit this to a three-term Fourier series. Does the Fourier series provide a good fit to your data? If so, what is the dominant term? Rationalize it. What is the second most important term? Rationalize your result. 

Transcribed Image Text:

- cosø) + V,(1 – cos 2ø) + V(O) = K(1 – cosø) + V,(1 – cos 20) + V;(1 – cos 30) = K(®) + V½(@) + Vz (@) %3! CH3 vs. CHз CHз ČH3 "Crowded" "Not crowded" ш