VSEPR (valence state electron pair repulsion) theory was formulated to anticipate the local geometry about an atom in a molecule (see discussion in Section 25.1). All that is required is the number of electron pairs surrounding the atom, broken down into bonded pairs and non-bonded (lone) pairs. For example, the carbon in carbon tetrafluoride is surrounded by four electron pairs, all of them tied up in CF

bonds, whereas the sulfur in sulfur tetra-fluoride is surrounded by five electron pairs, four of which are tied up in SF bonds with the fifth being a lone pair.

VSEPR theory is based on two simple rules. The first is that electron pairs (either lone pairs or bonds) will seek to avoid each other as much as possible. Thus, two electron pairs will lead to a linear geometry, three pairs to a trigonal planar geometry, four pairs to a tetrahedral geometry, five pairs to a trigonal bipyramidal geometry, and six pairs to an octahedral geometry. Although this knowledge is sufficient to assign a geometry for a molecule such as carbon tetra-fluoride (tetrahedral), it is not sufficient to specify the geometry of a molecule such as sulfur tetra-fluoride. Does the lone pair assume an equatorial position on the trigonal bipyramid leading to a seesaw geometry, or an axial position leading to a trigonal pyramidal geometry?

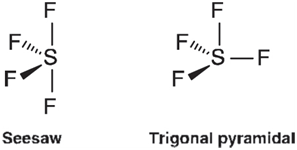
The second rule, that lone pairs take up more space than bonds, clarifies the situation. The seesaw geometry in which the lone pair is 90⁰ to two of the SF bonds and 120⁰ to the other two bonds is preferable to the trigonal pyramidal geometry in which three bonds are 90⁰ to the lone pair.

Although VSEPR theory is easy to apply, its results are strictly qualitative and often of limited value. For example, although the model tells us that sulfur tetrafluoride adopts a seesaw geometry, it does not reveal whether the trigonal pyramidal structure (or any other structure) is an energy minimum, and if it is, what its energy is relative to the seesaw form. Also it has little to say when more than six electron pairs are present. For example, VSEPR theory tells us that xenon hexafluoride is not octahedral, but it does not tell us what geometry the molecule actually assumes. Hartree€“Fock molecular orbital calculations provide an alternative.

a. Optimize the structure of SF4 in a seesaw geometry (C_2v symmetry) using the HF/3-21G model and calculate vibrational frequencies (the infrared spectrum). This calculation is necessary to verify that the energy is at a minimum. Next, optimize the geometry of SF₄ in a trigonal pyramidal geometry and calculate its vibrational frequencies. Is the seesaw structure an energy minimum? What leads you to your conclusion? Is it lower in energy than the corresponding trigonal pyramidal structure in accordance with VSEPR theory? What is the energy difference between the two forms? Is it small enough that both might actually be observed at room temperature? Is the trigonal pyramidal structure an energy minimum?

b. Optimize the geometry of XeF6 in an octahedral geometry (O_h symmetry) using the HF/3-21G model and calculate vibrational frequencies. Next, optimize XeF₆ in a geometry that is distorted from octahedral (preferably a geometry with C₁ symmetry) and calculate its vibrational frequencies. Is the octahedral form of XeF6 an energy minimum? What leads you to your conclusion? Does distortion lead to a stable structure of lower energy?

Transcribed Image Text:

F, S-F Fl.S Trigonal pyramidal Seesaw