Review Conceptual Example 11 before attempting to work this problem. The magnitude of each of the charges in Figure 18.20 is 8.60 × 10^‒12 C. The lengths of the sides of the rectangles are 3.00 cm and 5.00 cm. Find the magnitude of the electric field at the center of the rectangle in Figures 18.20a and b.

Conceptual Example 11

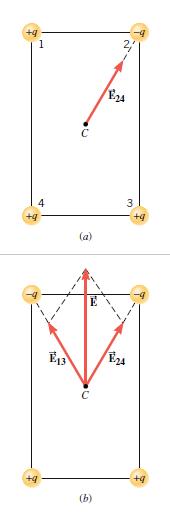
Four point charges all have the same magnitude, but they do not all have the same sign. These charges are fixed to the corners of a rectangle in two different ways, as Figure 18.20 shows. Consider the net electric field at the center C of the rectangle in each case. In which case, if either, is the net electric field greater?

(a) It is greater in Figure 18.20a.

(b) It is greater in Figure 18.20b.

(c) The field has the same magnitude in both cases.

Reasoning

The net electric field at C is the vector sum of the individual fields created there by the charges at each corner. Each of the individual fields has the same magnitude, since the charges all have the same magnitude and are equidistant from C. The directions of the individual fields are different, however. The field created by a positive charge points away from the charge, and the field created by a negative charge points toward the charge.

Answers (a) and (c) are incorrect. To see why these answers are incorrect, note that the charges on corners 2 and 4 are identical in both parts of Figure 18.20. Moreover, in Figure 18.20a the charges at corners 1 and 3 are both +q, so they contribute individual fields of the same magnitude at C that have opposite directions and, therefore, cancel. However, in Figure 18.20b the charges at corners 1 and 3 are ‒q and +q, respectively. They contribute individual fields of the same magnitude at C that have the same directions and do not cancel, but combine to produce the field E_(vector)13 shown in Figure 18.20b. The fact that this contribution to the net field at C is present in Figure 18.20b but not in Figure 18.20a means that the net fields in the two cases are different and that the net field in Figure 18.20a is less than (not greater than) the net field in Figure 18.20b.

Answer (b) is correct. To assess the net field at C, we need to consider the contribution from the charges at corners 2 and 4, which are ‒q and +q, respectively, in both cases. This is just like the arrangement on corners 1 and 3, which was discussed previously. It leads to a contribution to the net field at C that is shown as E_(vector)24 in both parts of the figure. In Figure 18.20a the net field at C is just E_(vector)24, but in Figure 18.20b it is the vector sum of E_(vector)13 and E_(vector)24, which is clearly greater than either of these two values alone.

Transcribed Image Text:

1 (a) +9 (b)