Review Conceptual Example 5 before attempting this problem. As the drawing shows, the length of a guitar string is 0.628 m. The frets are numbered for convenience. A performer can play a musical scale on a single string because the spacing between the frets is designed according to the following rule: When the string is pushed against any fret j, the fundamental frequency of the shortened string is larger by a factor of the twelfth root of two (¹²√ 2 ) than it is when the string is pushed against the fret j – 1. Assuming that the tension in the string is the same for any note, find the spacing

(a) Between fret 1 and fret 0 and

(b) Between fret 7 and fret 6.

Conceptual Example 5

Figure 17.18 shows the frets on the neck of a guitar. They allow the player to produce a complete sequence of musical notes using a single string. Starting with the fret at the top of the neck, each successive fret shows where the player should press to get the next note in the sequence. Musicians call the sequence the chromatic scale, and every thirteenth note in it corresponds to one octave, or a doubling of the sound frequency. Which describes the spacing between the frets? It is

(a) The same everywhere along the neck

(b) greatest at the top of the neck and decreases with each additional fret further on down toward the bridge (c) smallest at the top of the neck and increases with each additional fret further on down toward the bridge.

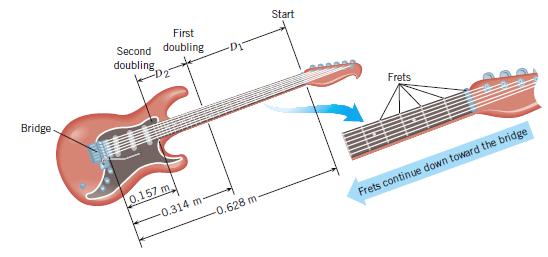
Reasoning Our reasoning is based on the relation f₁ = υ/(2L) (Equation 17.3, with n = 1). The value of n is 1 because a string vibrates mainly at its fundamental frequency when plucked, as mentioned in Example 4. This equation shows that L, which is the length between a given fret and the bridge of the guitar, is inversely proportional to the fundamental frequency f₁, or L = υ/(2 f₁). In Example 4 we found that the E string has a length of L = 0.628 m, corresponding to a fundamental frequency of f₁ = 164.8 Hz. We also found that the length between the bridge and the fret that must be pressed to double this frequency to 2 × 164.8 Hz = 329.6 Hz is one-half of 0.628 m, or L = 0.314 m. To understand the spacing between frets as one moves down the neck, consider the fret that must be pressed to double the frequency again, from 329.6 Hz to 659.2 Hz. The length between the bridge and this fret would be one-half of 0.314 m, or L = 0.157 m. Thus, the distances of the three frets that we have been discussing are 0.628 m, 0.314 m, and 0.157 m, as indicated in Figure 17.18. The distance D₁ between the first two of these frets is D₁ = 0.628 m – 0.314 m = 0.314 m. Similarly, the distance between the second and third of these frets is D₂ = 0.314 m – 0.157 m = 0.157 m.

Answers (a) and (c) are incorrect. The distances between the frets are shown in Figure 17.18. Clearly, the distances D₁ and D₂ are not equal, nor are they smaller at the top of the neck and greater further on down.

Answer (b) is correct. Figure 17.18 shows that D₁ is greater than D₂. Thus, the spacing between the frets is greatest at the top of the neck and decreases with each additional fret further on down.

Transcribed Image Text:

-0.628 m- 76 54 3210