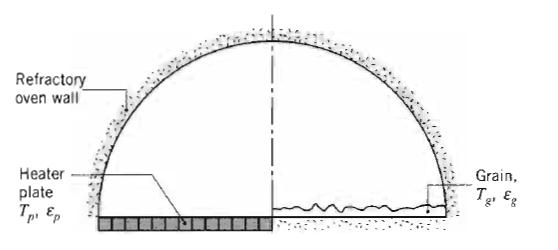
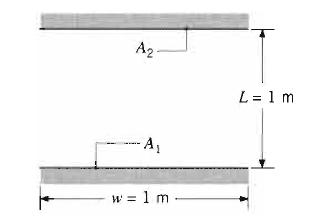
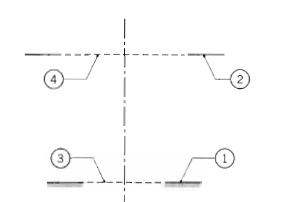
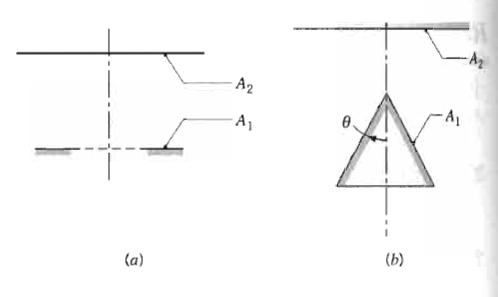
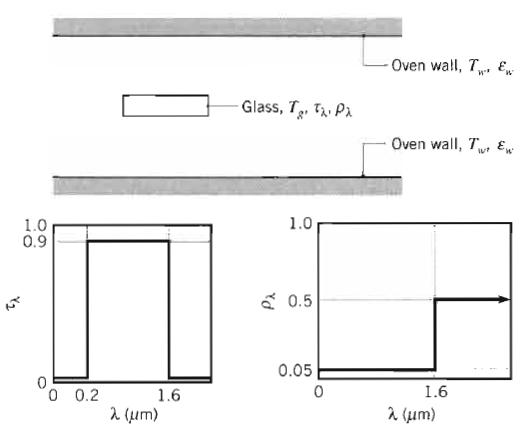
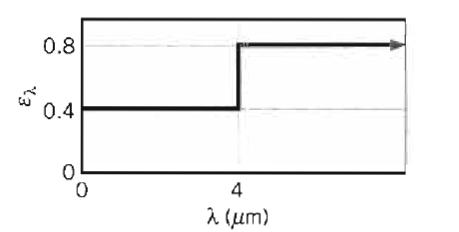
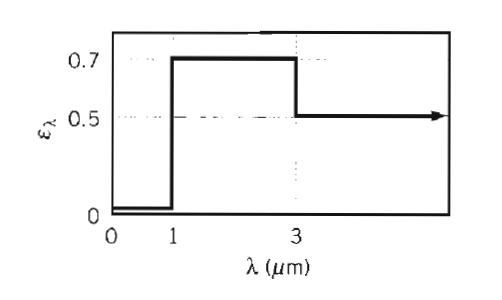
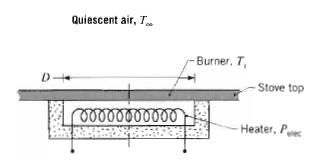
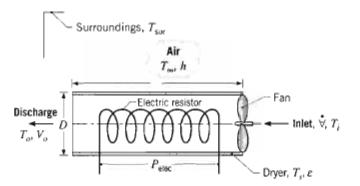
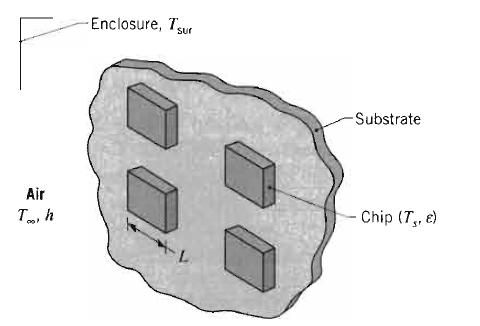
Fundamentals Of Momentum Heat And Mass Transfer 6th Edition James Welty, Gregory L. Rorrer, David G. Foster - Solutions
Discover comprehensive solutions for "Fundamentals Of Momentum Heat And Mass Transfer 6th Edition" by James Welty, Gregory L. Rorrer, and David G. Foster. Access a complete solution manual with step-by-step answers, solved problems, and an instructor manual to enhance your understanding. Download solutions in PDF format for free, offering an extensive test bank of questions and answers. Our online resource provides a detailed answers key, chapter solutions, and textbook insights, making learning more effective and convenient. Perfect for students seeking a reliable guide and free download for their academic journey.
![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()