Consider the general first-order linear equation y'(t) + a(t)y(t) = f(t). This equation can be solved, in
Question:
Consider the general first-order linear equation y'(t) + a(t)y(t) = f(t). This equation can be solved, in principle, by defining the integrating factor p(t) = exp(∫ a(t) dt). Here is how the integrating factor works. Multiply both sides of the equation by p (which is always positive) and show that the left side becomes an exact derivative. Therefore, the equation becomes
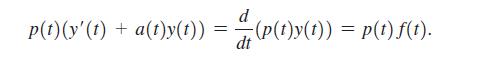
Now integrate both sides of the equation with respect to t to obtain the solution. Use this method to solve the following initial value problems. Begin by computing the required integrating factor.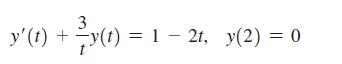
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Calculus For Scientists And Engineers Early Transcendentals
ISBN: 9780321849212
1st Edition
Authors: William L Briggs, Bernard Gillett, Bill L Briggs, Lyle Cochran
Question Posted:





