A basic property of definite integrals is their invariance under translation, as expressed by the equation The equation holds whenever is integrable and defined

A basic property of definite integrals is their invariance under translation, as expressed by the equation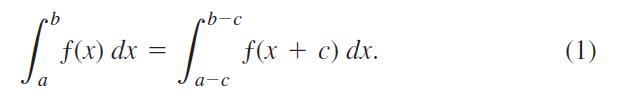

The equation holds whenever ƒ is integrable and defined for the necessary values of x. For example in the accompanying figure, show that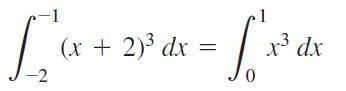

because the areas of the shaded regions are congruent.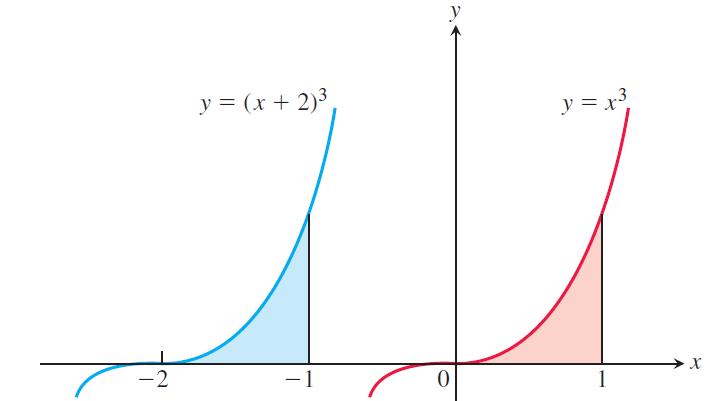

For each of the following functions, graph ƒ(x) over [a, b] and ƒ(x + c) over [a - c, b - c] to convince yourself that Equation (1) is reasonable.

a. ƒ(x) = x², a = 0, b = 1, c = 1

b. ƒ(x) = sin x, a = 0, b = π, c = π/2

c.

b [ - f(x) dx = a b-c a-c f(x + c) dx. (1)