A sequence of rational numbers is described as follows:

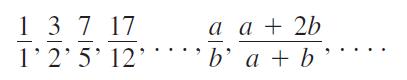
Here the numerators form one sequence, the denominators form a second sequence, and their ratios form a third sequence. Let x_n and y_n be, respectively, the numerator and the denominator of the nth fraction r_n = x_n/y_n.

a. Verify that x₁² - 2y₁² = -1, x₂² - 2y₂² = + 1 and, more generally, that if a² - 2b² = -1 or + 1, then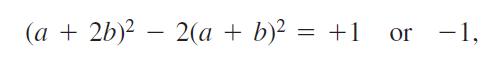

b. The fractions r_n = x_n/y_n approach a limit as n increases. What is that limit?

Transcribed Image Text:

1 3 7 17 1'2'5' 12 a a + 2b b' a + b