a. Show that the curvature of a smooth curve r(t) = (t)i + g(t)j defined by twice-differentiable

a. Show that the curvature of a smooth curve r(t) = ƒ(t)i + g(t)j defined by twice-differentiable functions x = ƒ(t) and y = g(t) is given by the formula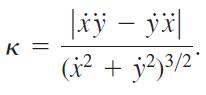

The dots in the formula denote differentiation with respect to t, one derivative for each dot. Apply the formula to find the curvatures of the following curves.

b. r(t) = t i + (ln sin t)j, 0

c. r(t) = [tan^-1 (sinh t)]i + (ln cosh t)j

Transcribed Image Text:

K= |xÿ – yx| (x² + y2)3/2