a. Suppose the graph of a continuous function (x) rises steadily as x moves from left to
Question:
a. Suppose the graph of a continuous function ƒ(x) rises steadily as x moves from left to right across an interval [a, b]. Let P be a partition of [a, b] into n subintervals of equal length Δx = (b - a)/n. Show by referring to the accompanying figure that the difference between the upper and lower sums for ƒ on this partition can be represented graphically as the area of a rectangle R whose dimensions are [ƒ(b) - ƒ(a) ] by Δx.
b. Suppose that instead of being equal, the lengths Δxk of the subintervals of the partition of [a, b] vary in size. Show that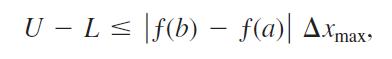
where Δxmax is the norm of P, and hence that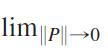
(U - L) = 0.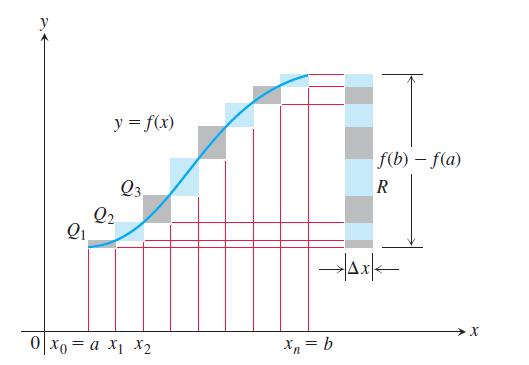
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Thomas Calculus Early Transcendentals
ISBN: 9780321884077
13th Edition
Authors: Joel R Hass, Christopher E Heil, Maurice D Weir
Question Posted:





