The fish and game department in a certain state is planning to issue hunting permits to control the deer population (one deer per permit). It is known that if the deer population falls below a certain level m, the deer will become extinct. It is also known that if the deer population rises above the carrying capacity M, the population will decrease back to M through disease and malnutrition.

a. Discuss the reasonableness of the following model for the growth rate of the deer population as a function of time: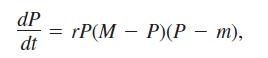

where P is the population of the deer and r is a positive constant of proportionality. Include a phase line.

b. Explain how this model differs from the logistic model dP/dt = rP(M - P) . Is it better or worse than the logistic model?

c. Show that if P > M for all t, then lim_t→∞ P(t) = M.

d. What happens if P

e. Discuss the solutions to the differential equation. What are the equilibrium points of the model? Explain the dependence of the steady-state value of P on the initial values of P. About how many permits should be issued?

dP dt rP(M P)(P m),