The Fundamental Theorem of Calculus for scalar functions of a real variable holds for vector functions of a real variable as well. Prove this by using the theorem for scalar functions to show first that if a vector function r(t) is continuous for a ≤ t ≤ b, then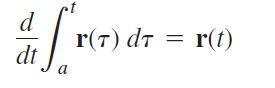

at every point t of (a, b). Then use the conclusion in part (b) of Exercise 41 to show that if R is any antiderivative of r on [a, b] then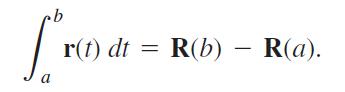

Data from Exercise 41

b. Use the result in part (a) to show that if R(t) is any antiderivative of r(t) on I, then any other antiderivative of r on I equals R(t) + C for some constant vector C.

Transcribed Image Text:

d a fr(7) r(7) dt = r(t) dt a