The formula

derived in Exercise 5, expresses the curvature k(x) of a twice-differentiable plane curve y = ƒ(x) as a function of x. Find the curvature function of each of the curves. Then graph ƒ(x) together with k(x) over the given interval. You will find some surprises.

y = sin x, 0 ≤ x ≤ 2π

Data from Exercise 5

The graph y = ƒ(x) in the xy-plane automatically has the parametrization x = x, y = ƒ(x), and the vector formula r(x) = xi + ƒ(x)j. Use this formula to show that if ƒ is a twice-differentiable function of x, then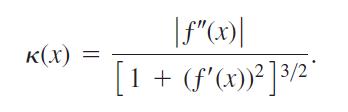

Use the formula for κ in part (a) to find the curvature of y = ln (cos x), -π/2

Transcribed Image Text:

K(X) = |f"(x)| [1 + (f'(x))²] 3³/2²