To escape Earth’s gravitational field, a rocket must be launched with an initial velocity called the escape velocity. A rocket launched from the surface of Earth has velocity v (in miles per second) given by

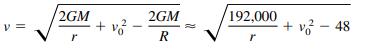
where v0 is the initial velocity, r is the distance from the rocket to the center of Earth, G is the gravitational constant, M is the mass of Earth, and R is the radius of Earth (approximately 4000 miles).

(a) Find the value of v0 for which you obtain an infinite limit for r as v approaches zero. This value of v0 is the escape velocity for Earth.

(b) A rocket launched from the surface of the moon has velocity v (in miles per second) given by

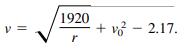
Find the escape velocity for the moon.

(c) A rocket launched from the surface of a planet has velocity v (in miles per second) given by

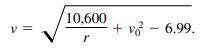
Find the escape velocity for this planet. Is the mass of this planet larger or smaller than that of Earth? (Assume that the mean density of this planet is the same as that of Earth.)

Transcribed Image Text:

V = 2GM r + v 2GM R /192,000 r +48