When a circle rolls externally along the circumference of a second, fixed circle, any point P on the circumference of the rolling circle describes an epicycloid, as shown here. Let the fixed circle have its center at the origin O and have radius a.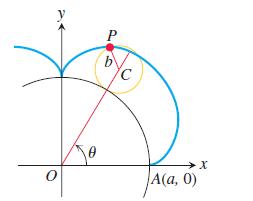

Let the radius of the rolling circle be b and let the initial position of the tracing point P be A(a, 0). Find parametric equations for the epicycloid, using as the parameter the angle θ from the positive x-axis to the line through the circles’ centers.

O P b C X A(a, 0)