A simple model for a multi path communications channel is shown in Figure 5.20(a).

Figure 5.20 (a)

(a) Find H_c (f) = Y(f) / X (f) for this channel and plot |H_c(f)| for β = 1 and 0.5.

(b) In order to equalize, or undo, the channel-induced distortion, an equalization filter is used. Ideally, its frequency response function should be 

H_eq (f) = 1 / H_c(f)

if the effects of noise are ignored and only distortion caused by the channel is considered. A tapped-delay-line or transversal filter, as shown in Figure 5.20(b), is commonly used to approximate H_eq (f). Write down a series expression for H'_eq (f) = Z(f) / Y(f).

Figure 5.20(b)

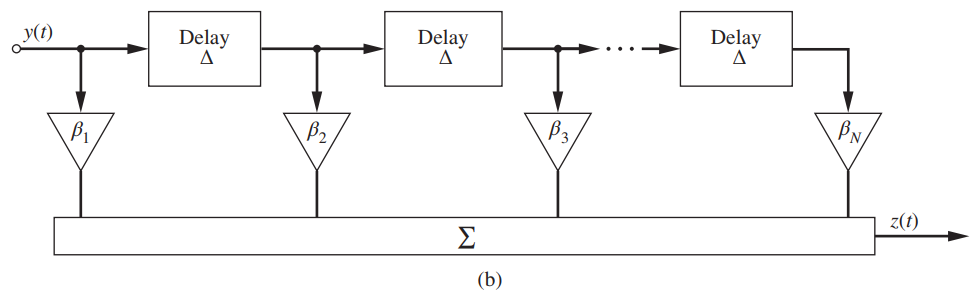
(c) Using (1 + x)^-1 = 1 - x + x² - x³ + ...,|x| < 1, find a series expression for 1/H_c(f). Equating this with H_eq (f) found in part (b), find the values for β₁, β₂,...., β_N, assuming Ï„_m = Δ.

() x(t) ) Delay Gain x(t ,) Tm (a) () Delay Delay Delay B2 PN z(t) (b)