An ideal finite-time integrator is characterized by the input-output relationship

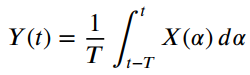
(a) Justify that its impulse response is h(t) = 1 / T [u (t) - u (t - T)].

(b) Obtain its frequency response function. Sketch it.
(c) The input is white noise with two-sided power spectral density N₀/2. Find the power spectral density of the output of the filter.

(d) Show that the auto correlation function of the output is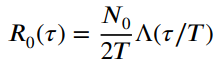 

where Λ(x) is the unit-area triangular function defined in Chapter 2. 

(e) What is the equivalent noise bandwidth of the integrator?
(f) Show that the result for the output noise power obtained using the equivalent noise bandwidth found in part (e) coincides with the result found from the auto correlation unction of the output found in part (d).

Y (t) = X () d t-T No A(7/T) R,(7) =