Assume a biphase modulated signal in white Gaussian noise of the form y(t) = 2P sin (Ï
Question:
y(t) = ˆš2P sin (ωct ± cos-1 m + θ) + n(t), 0 ‰¤ t ‰¤ Ts
where the ± signs are equally probable and θ is to be estimated by a maximum-likelihood procedure. In the preceding equation,
Ts = signaling interval
P = average signal power
ωc = carrier frequency (rad/s)
m = modulation constant
θ = RF phase (rad)
Let the double-sided power spectral density of n(t) be 1/2 N0.
(a) Show that the signal portion of y(t) can be written as
S(t)= ˆš2Pm sin(ωct + θ) ± ˆš2P ˆš1- m2 cos(ωct + θ)
Write in terms of the orthonormal functions Ï•1 and Ï•2, given by (11.192) and (11.193).
(b) Show that the likelihood function can be written as 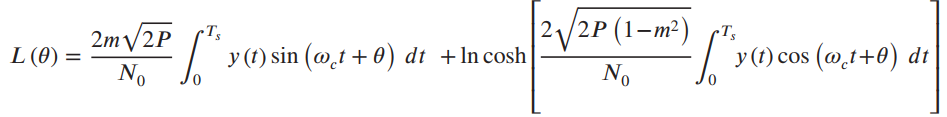 (c) Draw a block diagram of the ML estimator for θ and compare with the block diagram shown in Figure 11.15.
(c) Draw a block diagram of the ML estimator for θ and compare with the block diagram shown in Figure 11.15.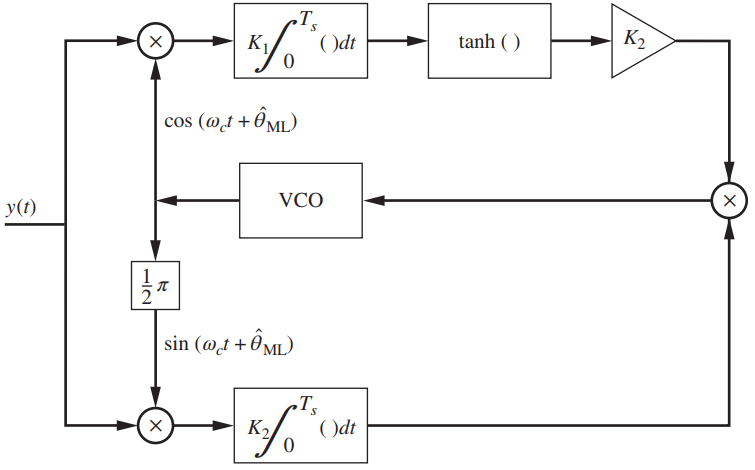
Step by Step Answer:

Principles of Communications Systems, Modulation and Noise
ISBN: 978-8126556793
7th edition
Authors: Rodger E. Ziemer, William H. Tranter





