Consider vertices-of-a-hyper-cube signaling, for which the in which the coefficients α ik are permuted through the values
Question:
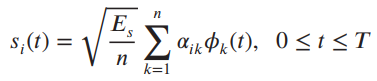
in which the coefficients αik are permuted through the values +1 and -1, Es is the signal energy, and the ϕks
are orthonormal. Thus, M = 2n, where n = log2 M is an integer. For M = 8, n = 3, the signal points in signal space lie on the vertices of a cube in three-space.
(a) Sketch the optimum partitioning of the observation space for M = 8.
(b) Show that for M = 8 the symbol error probability
PE = 1 - P(C)
where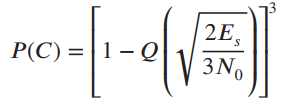
(c) Show that for n arbitrary the probability of symbol error is
PE = 1 - P(C)
where
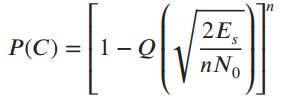
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Principles of Communications Systems, Modulation and Noise
ISBN: 978-8126556793
7th edition
Authors: Rodger E. Ziemer, William H. Tranter
Question Posted:





