The general definition of a matched filter is a filter that maximizes peak signal-to-rms noise at some prechosen instant of time t₀.

(a) Assuming white noise at the input, use Schwarz€™s inequality to show that the frequency response function of the matched filter is

H_m(f) = S*(f) exp(-j2Ï€ft₀)

where S(f) = i[s(t)] and s(t) is the signal to which the filter is matched.

(b) Show that the impulse response for the matched-filter frequency response function found in part (a) is

h_m(t) = s(t₀ - t)

(c) If s(t) is not zero t > t₀, the matched-filter impulse response is nonzero for t < 0; that is, the filter is non-causal and cannot be physically realized because it responds before the signal is applied. If we want a realizable filter, we use 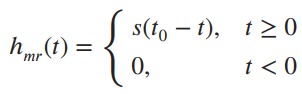Find the realizable matched-filter impulse response corresponding to the signal 

s(t) = AII[(t - T/2)/T]

and t₀ equal to 0, T/2, T, and 2T.

(d) Find the peak output signal for all cases in part (c). Plot them versus t₀. What do you conclude about the relation between t₀ and the causality condition?

Transcribed Image Text:

s(to – t), t> 0 t < 0 hm,(t) = %3D