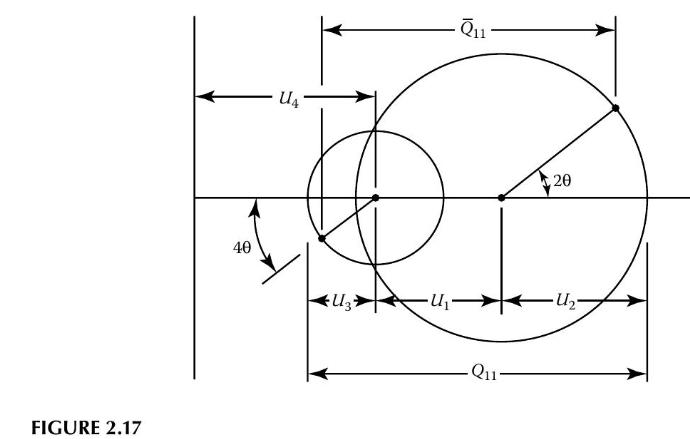
Describe the measurements that would have to be taken and the equations that would have to be used to determine \(G_{23}, v_{32}\), and \(E_{2}\) for a specially orthotropic, transversely isotropic material from a single tensile test. can be represented graphically by using two Mohr's circles, as shown in Figure 2.17. The distance between points on each of the two circles represents the total stiffness \(\bar{Q}_{11}\), whereas the distance between the centers of the two circles is given by \(U_{1}\). The radius and angle associated with one circle are \(U_{2}\) and \(2 \theta\), respectively, and the radius and angle associated with the other circle are \(U_{3}\) and \(4 \theta\), respectively. Thus, the distance between the centers of the circles is a measure of the isotropic component of stiffness, whereas the radii of the circles indicate the strength of the orthotropic component. If \(U_{2}=U_{3}=0\), the circles collapse to points and the material is isotropic.
Invariants will prove to be very useful later in the analysis of randomly oriented short fiber composites and laminated plates. For additional applications of invariants in composite analysis, the reader is referred to books by Halpin [5] and Tsai and Hahn [11].

Transcribed Image Text:

FIGURE 2.17 40 U4 Qu' 20 U3 U -U- Q11