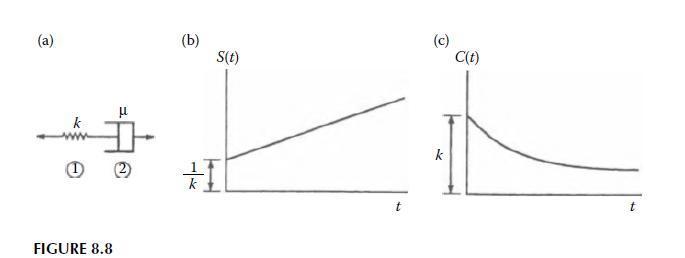
Question: For the Maxwell model shown in Figure 8.8, it can be shown that the complex modulus is given by [E^{*}(omega)=E^{prime}(omega)[1+i eta(omega)]] where the frequency-dependent storage
For the Maxwell model shown in Figure 8.8, it can be shown that the complex modulus is given by
\[E^{*}(\omega)=E^{\prime}(\omega)[1+i \eta(\omega)]\]
where the frequency-dependent storage modulus is given by
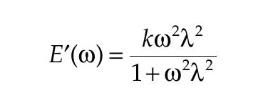
and the frequency-dependent loss factor is given by
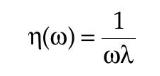
where \(\omega\) is the frequency and \(\lambda=\mu / k\) is the relaxation time. Let us assume that the Maxwell model adequately describes the viscoelastic behavior of a particular material. Explain how you would use the Maxwell model and frequency-domain vibration test data to indirectly determine the numerical value of the relaxation modulus \(C(t)\) for this material.
E'(@): kw 1+w222
Step by Step Solution
3.34 Rating (145 Votes )
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


