The stiffness matrix ([C]) for a specially orthotropic material associated with the principal material axes ((1,2,3)) is
Question:
The stiffness matrix \([C]\) for a specially orthotropic material associated with the principal material axes \((1,2,3)\) is given in Equation 2.16. Prove that, when the material is specially orthotropic and transversely isotropic in the 2-3 planes (i.e., the properties are invariant to rotations about the 1 axis) the stiffness matrix [C] is given by Equation 2.17. To prove that \(C_{44}=\left(C_{22}-C_{23}\right) / 2\), consider the stresses and strains acting on an element under pure shear stress \(\sigma_{23}\) and the corresponding stresses and strains acting on the same element, which has been rotated by a convenient angle in the \(2-3\) planes.
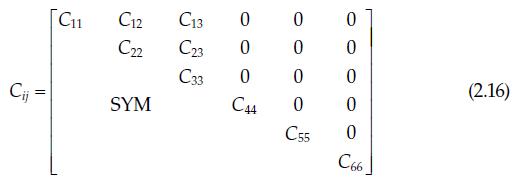
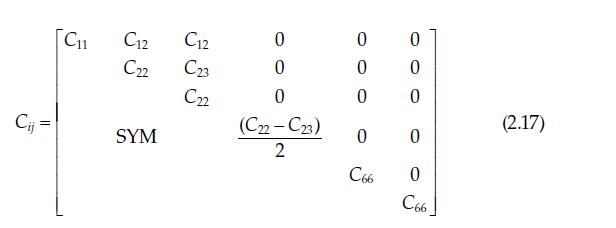
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Principles Of Composite Material Mechanics
ISBN: 9781498720694
4th Edition
Authors: Ronald F. Gibson
Question Posted:





