This exercise is regarding the special case of block-bootstrapping the sample mean, discussed in Section 14.5.

(i) Show that the influence function IF defined in (A2) [above (14.72)] is given by IF(x, F) = x − μ, where μ = E(Xt ).

(ii) Show that the bootstrap statistic can be expressed as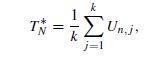

where the Un,j ’s are i.i.d. uniformly distributed among the points ui = l −1(Xi+1 + · · · + Xi+l), i = 0, . . . , n − l. Thus, in particular, the conditional mean and variance of T ∗
N given X1, . . . , XN are given by (14.73) and (14.74), respectively.

Transcribed Image Text:

= k k j=1 Un.j