22. (The Wallet Paradox) Consider the following “paradox” given by Martin Gardner in his book Aha! Gotcha (W. H. Freeman and Company, New York, 1981).

Each of two persons places his wallet on the table. Whoever has the smallest amount of money in his wallet, wins all the money in the other wallet. Each of the players reason as follows: “I may lose what I have but I may also win more than I have. So the game is to my advantage.”

As Kent G. Merryfield, Ngo Viet, and SaleemWatson have observed in their paper “The Wallet Paradox” in the August–September 1997 issue of the American Mathematical Monthly, Paradoxically, it seems that the game is to the advantage of both players.
. . . However, the inference that “the game is to my advantage” is the source of the apparent paradox, because it does not take into account the probabilities of winning or losing. In other words, if the game is played many times, how often does a player win? How often does he lose? And by how much?
Following the analysis of Kent G. Merryfield, Ngo Viet, and Saleem Watson, let X and Y be the amount of money in the wallets of players A and B, respectively. Let WA and WB be the amount of money that player A and B will win, respectively. WA(X, Y ) = −WB(X, Y ) and

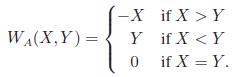
Suppose that the distribution function of the money in each player’s wallet is the same;
that is, X and Y are independent, identically distributed random variables on some interval [a, b] or [a,∞), 0 ≤ a

Transcribed Image Text:

-X if X>Y WA(X,Y) = Y if X