31. In this exercise, we will outline a third technique for solving Example 3.34: We draw cards, one at a time, at random and successively from an ordinary deck of 52 cards with replacement.What is the probability that an ace appears before a face card?

Hint: Consider a Markov chain {Xn : n = 1, 2, . . .} with state space {1, 2, 3} and transition probability matrix

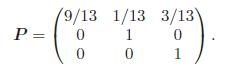
The relation between the problem we want to solve and the Markov chain {Xn : n = 1, 2, . . .} is as follows: As long as a non-ace, non-face card is drawn, the Markov chain remains in state 1. If an ace is drawn before a face card, it enters the absorbing state 2 and will remain there indefinitely. Similarly, if a face card is drawn before an ace, the process enters the absorbing state 3 and will remain there forever. Let An be the event that the Markov chain moves from state 1 to state 2 in n steps. Show that

and calculate the desired probability

by applying Theorem 1.8:

Transcribed Image Text:

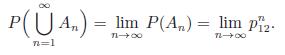
/9/13 1/13 3/13 P = 0 1 0 0 0 1