5.5.7 Consider a collection of circles in the plane whose centers are distributed according to a spatial Poisson process with parameter jAj, where jAj denotes the area of the set A. (In particular, the number of centers .A/ in the set A follows the distribution law Prf.A/ D kg D e????jA

.jAj/k=k!

.) The radius of each circle is assumed to be a random variable independent of the location of the center of the circle, with density function f .r/ and finite second moment.

(a) Show that C.r/, defined to be the number of circles that cover the origin and have centers at a distance less than r from the origin, determines a variabletime Poisson process, where the time variable isnowtaken to be the distance r.

Hint: Prove that an event occurring between r and rCdr (i.e., there is a circle that covers the origin and whose center is in the ring of radius r to rCdr) has probability 2r dr R1 r f ./d Co.dr/, and events occurring over disjoint intervals constitute independent random variables. Show that C.r/ is a variable-time (nonhomogeneous) Poisson process with parameter

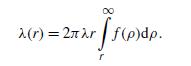
(b) Show that the number of circles that cover the origin is a Poisson random variable with parameter

Transcribed Image Text:

2 (r) = 2rff(p)dp. f