8.1.6 Manufacturers of crunchy munchies such as cheese crisps use compression testing machines to gauge product quality. The crisp, or whatever, is placed between opposing plates, which then move together. As the crisp is crunched, the force is measured as a function of the distance that the plates have moved. The output of the compression testing machine is a graph of force versus distance that is much like Figure 8.3. What aspects of the graph might be measures of product quality?

Model the test as a row of tiny balloons between parallel plates. Each single balloon might follow a force–distance behavior of the form D Ke.1????q.e//, where is the force, K is Young’s modulus, e is strain or distance, and q.e/ is a function that measures departures from Hooke’s law, to allow for soggy crisps.

Each balloon obeys this relationship up until the random strain at which it bursts. Determine the mean force as a function of strain. Use F.x/ for the cumulative distribution function of failure strain

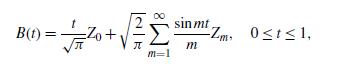
is a standard Brownian motion for 0 t 1. Try to simulate a Brownian motion stochastic process, at least approximately, by using finite sums of the form

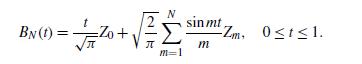
If B.t/;0 t 1, is a standard Brownian motion on the interval [0; 1], then B0.t/ D .1Ct/B.1=.1Ct//;0 t

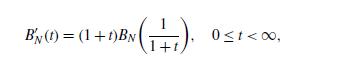
as an approximate standard Brownian motion. In what ways do these finite approximations behave like Brownian motion? Clearly, they are zero mean Gaussian processes. What is the covariance function, and how does it compare to that of Brownian motion? Do the gambler’s ruin probabilities of (8.13)
accurately describe their behavior? It is known that the squared variation of a Brownian motion stochastic process is not random, but constant:

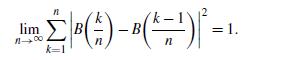
This is a further consequence of the variance relation E
.1B/2
D 1t (see the remark in Section 8.1.2). To what degree do the finite approximations meet this criterion?

Transcribed Image Text:

B(t)= = m=1 sin mt m Zm 0t1,