a) Let (d(x, A):=inf _{a in A}|x-a|) be the distance between the point (x in mathbb{R}^{d}) and
Question:
a) Let \(d(x, A):=\inf _{a \in A}|x-a|\) be the distance between the point \(x \in \mathbb{R}^{d}\) and the set \(A \in \mathscr{B}\left(\mathbb{R}^{d}\right)\). Show that \(x \mapsto d(x, A)\) is continuous.
b) Let \(u_{n}\) be as in (7.7). Show that \(u_{n} \in \mathcal{C}_{c}\left(\mathbb{R}^{d}\right)\) and \(\inf _{n} u_{n}(x)=\mathbb{1}_{K}(x)\). Draw a picture if \(d=1\) and \(K=[0,1]\).
c) Let \(\chi_{n}\) be a sequence of type \(\delta\), i.e. \(\chi_{n} \in \mathcal{C}_{c}^{\infty}\left(\mathbb{R}^{d}\right)\), \(\operatorname{supp} \chi_{n} \subset \mathbb{B}(0,1 / n), \chi_{n} \geqslant 0\) and \(\int \chi_{n}(x) d x=1\). Show that \(v_{n}:=\chi_{n} \star u_{n} \in \mathcal{C}_{c}^{\infty}\left(\mathbb{R}^{d}\right)\) are smooth functions such that \(\lim _{n \rightarrow \infty} v_{n}=\mathbb{1}_{K}\).
Data From (7.7)
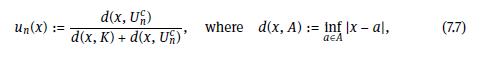
Step by Step Answer:

Brownian Motion A Guide To Random Processes And Stochastic Calculus De Gruyter Textbook
ISBN: 9783110741254
3rd Edition
Authors: René L. Schilling, Björn Böttcher




