Define the stochastic process ({X(t), t in mathbf{R}}) by [X(t)=A cos (omega t+Phi)] where (A) and (Phi)
Question:
Define the stochastic process \(\{X(t), t \in \mathbf{R}\}\) by
\[X(t)=A \cos (\omega t+\Phi)\]
where \(A\) and \(\Phi\) are independent random variables with \(E(A)=0\) and \(\Phi\) is uniformly distributed over the interval \([0,2 \pi]\).
Check whether the covariance function of the weakly stationary process \(\{X(t), t \in \mathbf{R}\}\) can be obtained from the limit relation (12.5).
The covariance function of a slightly more general process has been determined in example 6.6 at page 235 .
Data from Example 6.6
In modifying example 6.3, let

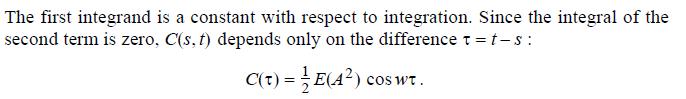
Thus, the process is weakly stationary.
Data from 12.5
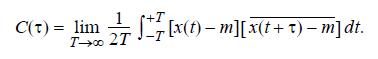
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Applied Probability And Stochastic Processes
ISBN: 9780367658496
2nd Edition
Authors: Frank Beichelt
Question Posted:





