Let f (x 1 ,x 2 ) be the density of a r.vec X = (X 1
Question:
Let f (x1,x2) be the density of a r.vec X = (X1,X2). We call a curve in a (x1,x2)-plane a level curve if it is determined by an equation f (x1,x2) = c, where c is a constant. Argue that all points in this curve are equally likely to be values of X. Show that for a bivariate normal distribution, the level curves are ellipses. Graph typical level curves for the following covariance matrices: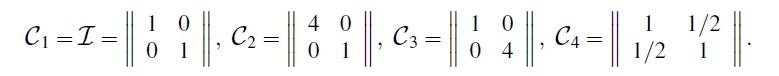
Describe verbally an analogous picture for the case of a larger dimension.
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:





