Let (left(B_{t} ight)_{t geqslant 0}, d_{t}) and (g_{t}) be as in Corollary 11.26. Define [L_{t}^{-}:=t-g_{t} quad text
Question:
Let \(\left(B_{t}\right)_{t \geqslant 0}, d_{t}\) and \(g_{t}\) be as in Corollary 11.26. Define
\[L_{t}^{-}:=t-g_{t} \quad \text { and } \quad L_{t}:=d_{t}-g_{t}\]
Find the laws of \(\left(L_{t}^{-}, L_{t}\right), L_{t}^{-}, L_{t}\) and \(L_{t}\) conditional on \(L_{t}^{-}=r\).
Find the probability that \(\mathbb{P}\left(L_{t}>r+s \mid L_{t}^{-}=r\right)\), i.e. the probability that an excursion continues for \(s\) units of time if we know that it is already \(r\) units of time under way.
Data From Corollary 11.26

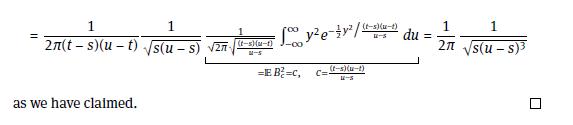
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Brownian Motion A Guide To Random Processes And Stochastic Calculus De Gruyter Textbook
ISBN: 9783110741254
3rd Edition
Authors: René L. Schilling, Björn Böttcher
Question Posted:





