Let (left(B_{t}, mathscr{F}_{t} ight)_{t geqslant 0}) be a one-dimensional Brownian motioin and (tau) a stopping time. Show
Question:
Let \(\left(B_{t}, \mathscr{F}_{t}\right)_{t \geqslant 0}\) be a one-dimensional Brownian motioin and \(\tau\) a stopping time. Show that \(f(s, \omega):=\mathbb{1}_{[0, T \wedge \tau(\omega))}(s), 0 \leqslant s \leqslant T
Data From 15.15 Theorem
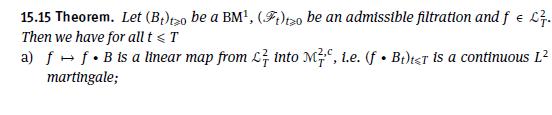

Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Brownian Motion A Guide To Random Processes And Stochastic Calculus De Gruyter Textbook
ISBN: 9783110741254
3rd Edition
Authors: René L. Schilling, Björn Böttcher
Question Posted:





