Use Theorem 15.15.c) to show that the stochastic integrals for the right and left continuous simple processes
Question:
Use Theorem 15.15.c) to show that the stochastic integrals for the right and left continuous simple processes \(f(t, \omega):=\sum_{j=1}^{n} \phi_{j-1}(\omega) \mathbb{1}_{\left[s_{j-1}, s_{j}\right)}(t)\) and \(g(t, \omega):=\) \(\sum_{j=1}^{n} \phi_{j-1}(\omega) \mathbb{1}_{\left(s_{j-1}, s_{j}\right]}(t)\) coincide.
Data From Theorem 15.15
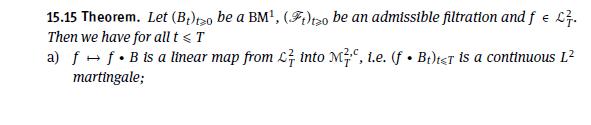



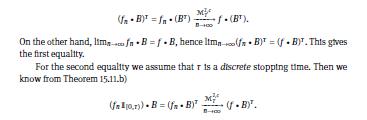

Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Brownian Motion A Guide To Random Processes And Stochastic Calculus De Gruyter Textbook
ISBN: 9783110741254
3rd Edition
Authors: René L. Schilling, Björn Böttcher
Question Posted:





