Let (left(N_{t} ight)_{t geqslant 0}) be a Poisson process with intensity (lambda=1) (see Problem 10.1 for the
Question:
Let \(\left(N_{t}\right)_{t \geqslant 0}\) be a Poisson process with intensity \(\lambda=1\) (see Problem 10.1 for the definition). Show that for \(\mathscr{F}_{t}^{N}:=\sigma\left(N_{r}: r \leqslant t\right)\) both \(X_{t}:=N_{t}-t\) and \(X_{t}^{2}-t\) are martingales. Explain why this does not contradict Theorem 19.5.
Data From Theorem 19.5


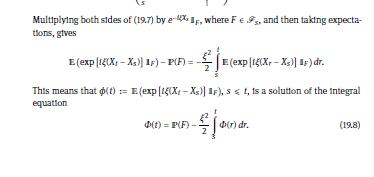
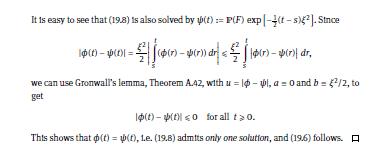
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Brownian Motion A Guide To Random Processes And Stochastic Calculus De Gruyter Textbook
ISBN: 9783110741254
3rd Edition
Authors: René L. Schilling, Björn Böttcher
Question Posted:





