Similar to Example 2.2-7c, prove that the probability of selecting a red ball at any draw is the same as at the first draw.

 Example 2.2-7c

There are exactly two participants in a contest that consists in answering questions. The first contestant chooses at random one question out of eight, and after that the second contestant chooses a question out of the seven remaining. (Regarding the general terminology, we say that an element is selected from a set of elements at random, if all elements are equally likely to be selected.) There are three easy and five difficult questions. Which contestant has an advantage: the first or the second? We will get an answer at the end of this example, but first consider a general scheme which is used for this type of problem.

(c) Two balls are drawn at random without replacement. What is the probability that the second ball is red (whatever the first is)? The answer, which perhaps looks somewhat unexpected, is that this probability is the same as it would be for the first ball: r. Thus, no contestant in the above problem has an advantage. 

To make it more plausible, note that it is equally likely to select first a red ball and then a black one, or first, a black and then a red. Indeed, the number of combinations of the former type is rb, and of the latter type br. Since the sample space is the same as in Problem (b), |Ω| is still n(n−1), and hence, the probabilities of both events are the same:

Let us derive rigorously the probability that the second ball is red. There are r(r −1) ways to select two red balls, and there are br ways to select a black ball first, and after that a red ball. Then, for the event A in hand, |A| = r(r−1) + br = r(r + b − 1) = r(n − 1).

Hence,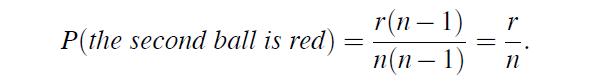

(Another way of reasoning is to observe that there are r ways to select a red ball which will be the second, and for each such a selection, there are n−1 ways to select any ball out of the remaining n−1. So, again |A| = r(n−1).)

After we consider a counting technique in Section 3, in Exercise 21, the reader will be invited to prove a similar result for an arbitrary draw.

Transcribed Image Text:

br n(n-1)