Suppose X₁, . . . , X_nis an independent sequence of exponential random variables with parameter λ = 1. Let

 Z = max(X₁, . . . , X_n) ˆ’ log n.

(a) Show that the cdf of Z is

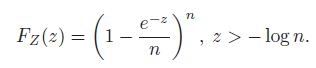
(b) Show that for all z, 

The limit is a probability distribution called an extreme value distribution. It is used in many fields which model extreme values, such as hydrology (intense rainfall), actuarial science, and reliability theory.

(c) Suppose the times between heavy rainfalls are independent and have an exponential distribution with mean 1 month. Find the probability that in the next 10 years, the maximum time between heavy rainfalls is greater than 3 months in duration.

Transcribed Image Text:

Fz(e) = (1-) Fz(2) = , 2 > - log n. Fz(2) → e-e-² as n → oo.