Sue Reynolds has to decide if she should get information (at a cost of $20,000) to help
Question:
Sue Reynolds has to decide if she should get information
(at a cost of $20,000) to help her decide whether to invest in a retail store. If she gets the information, there is a 0.6 probability that the information will be favorable and a 0.4 probability that the information will not be favorable. If the information is favorable, there is a 0.9 probability that the store will be a success. If the information is not favorable, the probability of a successful store is only 0.2. Without any information, Sue estimates that the probability of a successful store will be 0.6. A successful store will give a return of $100,000. If the store is built but is not successful, Sue will see a loss of $80,000. Of course, she could always decide not to build the retail store.
(a) What do you recommend?
(b) What impact would a 0.7 probability of obtaining favorable information have on Sue’s decision?
The probability of obtaining unfavorable information would be 0.3.
(c) Sue believes that the probabilities of a successful and an unsuccessful retail store, given favorable information, might be 0.8 and 0.2, respectively, instead of 0.9 and 0.1, respectively. What impact, if any, would this have on Sue’s decision and the best EMV?
(d) Sue had to pay $20,000 to get information.
Would her decision change if the cost of the information increased to $30,000?
(e) Using the data in this problem and the following utility table, compute the expected utility. Is this the curve of a risk seeker or a risk avoider?
(f) Compute the expected utility given the following utility table. Does this utility table represent a risk seeker or a risk avoider?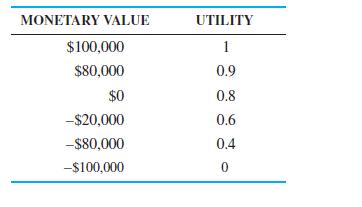
Step by Step Answer:

Quantitative Analysis For Management
ISBN: 9781292217659
13th Global Edition
Authors: Barry Render, Ralph M. Stair, Michael Hanna, Trevor Hale





